深入理解FFM原理

FM 和 FFM 模型是最近几年提出的模型，凭借其在数据量比较大并且特征稀疏的情况下，仍然能够得到优秀的性能和效果的特性，屡次在各大公司举办的 CTR 预估比赛中获得不错的战绩。美团技术团队在搭建 DSP 的过程中，探索并使用了 FM 和 FFM 模型进行 CTR 和 CVR 预估，并且取得了不错的效果。本文旨在把我们对 FM 和 FFM 原理的探索和应用的经验介绍给有兴趣的读者。

在计算广告领域，点击率 CTR（click-through rate）和转化率 CVR（conversion rate）是衡量广告流量的两个关键指标。准确的估计 CTR、CVR 对于提高流量的价值，增加广告收入有重要的指导作用。预估 CTR/CVR，业界常用的方法有人工特征工程 + LR(Logistic Regression)、GBDT(Gradient Boosting Decision Tree) + LR[1][2][3]、FM（Factorization Machine）[2][7]和 FFM（Field-aware Factorization Machine）[9]模型。在这些模型中，FM 和 FFM 近年来表现突出，分别在由 Criteo 和 Avazu 举办的 CTR 预测竞赛中夺得冠军 [4][5]。

考虑到 FFM 模型在 CTR 预估比赛中的不俗战绩，美团技术团队在搭建 DSP（Demand Side Platform）[6]平台时，在站内 CTR/CVR 的预估上使用了该模型，取得了不错的效果。本文是基于对 FFM 模型的深度调研和使用经验，从原理、实现和应用几个方面对 FFM 进行探讨，希望能够从原理上解释 FFM 模型在点击率预估上取得优秀效果的原因。因为 FFM 是在 FM 的基础上改进得来的，所以我们首先引入 FM 模型，本文章节组织方式如下：

首先介绍 FM 的原理。
其次介绍 FFM 对 FM 的改进。
然后介绍 FFM 的实现细节。
最后介绍模型在 DSP 场景的应用。

FM（Factorization Machine）是由 Konstanz 大学 Steffen Rendle（现任职于 Google）于 2010 年最早提出的，旨在解决稀疏数据下的特征组合问题 [7]。下面以一个示例引入 FM 模型。假设一个广告分类的问题，根据用户和广告位相关的特征，预测用户是否点击了广告。源数据如下 [8]

Clicked?	Country	Day	Ad_type
1	USA	26/11/15	Movie
0	China	1/7/14	Game
1	China	19/2/15	Game

“Clicked?“是 label，Country、Day、Ad_type 是特征。由于三种特征都是 categorical 类型的，需要经过独热编码（One-Hot Encoding）转换成数值型特征。

Clicked?	Country=USA	Country=China	Day=26/11/15	Day=1/7/14	Day=19/2/15	Ad_type=Movie	Ad_type=Game
1	1	0	1	0	0	1	0
0	0	1	0	1	0	0	1
1	0	1	0	0	1	0	1

由上表可以看出，经过 One-Hot 编码之后，大部分样本数据特征是比较稀疏的。上面的样例中，每个样本有 7 维特征，但平均仅有 3 维特征具有非零值。实际上，这种情况并不是此例独有的，在真实应用场景中这种情况普遍存在。例如，CTR/CVR 预测时，用户的性别、职业、教育水平、品类偏好，商品的品类等，经过 One-Hot 编码转换后都会导致样本数据的稀疏性。特别是商品品类这种类型的特征，如商品的末级品类约有 550 个，采用 One-Hot 编码生成 550 个数值特征，但每个样本的这 550 个特征，有且仅有一个是有效的（非零）。由此可见，数据稀疏性是实际问题中不可避免的挑战。

One-Hot 编码的另一个特点就是导致特征空间大。例如，商品品类有 550 维特征，一个 categorical 特征转换为 550 维数值特征，特征空间剧增。

同时通过观察大量的样本数据可以发现，某些特征经过关联之后，与 label 之间的相关性就会提高。例如，“USA”与 “Thanksgiving”、“China” 与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自 “China” 的用户很可能会在 “Chinese New Year” 有大量的浏览、购买行为，而在 “Thanksgiving” 却不会有特别的消费行为。这种关联特征与 label 的正向相关性在实际问题中是普遍存在的，如 “化妆品” 类商品与 “女” 性，“球类运动配件”的商品与 “男” 性，“电影票”的商品与 “电影” 品类偏好等。因此，引入两个特征的组合是非常有意义的。

多项式模型是包含特征组合的最直观的模型。在多项式模型中，特征 xixi x_i 和 xjxj x_j 的组合采用 xixjxixj x_i x_j 表示，即 xixi x_i 和 xjxj x_j 都非零时，组合特征 xixjxixj x_i x_j 才有意义。从对比的角度，本文只讨论二阶多项式模型。模型的表达式如下

y(x)=w0+∑i=1nwixi+∑i=1n∑j=i+1nwijxixj(1)(1)y(x)=w0+∑i=1nwixi+∑i=1n∑j=i+1nwijxixj y(\mathbf{x}) = w0+ \sum{i=1}^n wi x_i + \sum{i=1}^n \sum{j=i+1}^n w{ij} x_i x_j \label{eq:poly}\tag{1}

其中，nn n 代表样本的特征数量，xixi xi 是第 ii i 个特征的值，w0w0 w_0 、wiwi w_i 、wijwij w{ij} 是模型参数。

从公式 (1)(1)\eqref{eq:poly}可以看出，组合特征的参数一共有 n(n−1)2n(n−1)2 \frac{n(n-1)}{2} 个，任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。其原因是，每个参数 wijwij w{ij} 的训练需要大量 xixi x_i 和 xjxj x_j 都非零的样本；由于样本数据本来就比较稀疏，满足 “xixi x_i 和 xjxj x_j 都非零” 的样本将会非常少。训练样本的不足，很容易导致参数 wijwij w{ij} 不准确，最终将严重影响模型的性能。

那么，如何解决二次项参数的训练问题呢？矩阵分解提供了一种解决思路。在 model-based 的协同过滤中，一个 rating 矩阵可以分解为 user 矩阵和 item 矩阵，每个 user 和 item 都可以采用一个隐向量表示 [8]。比如在下图中的例子中，我们把每个 user 表示成一个二维向量，同时把每个 item 表示成一个二维向量，两个向量的点积就是矩阵中 user 对 item 的打分。

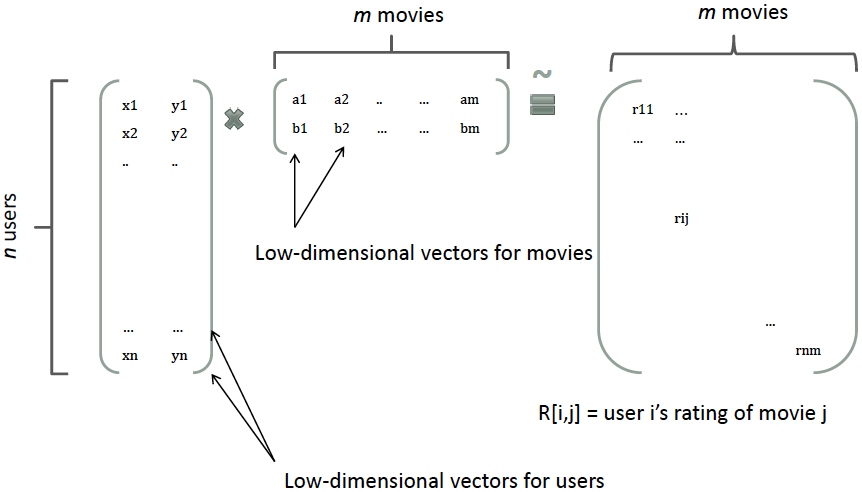
类似地，所有二次项参数 wijwij w{ij} 可以组成一个对称阵 WW \mathbf{W} （为了方便说明 FM 的由来，对角元素可以设置为正实数），那么这个矩阵就可以分解为 W=VTVW=VTV \mathbf{W} = \mathbf{V}^T \mathbf{V} ，VV \mathbf{V} 的第 jj j 列便是第 jj j 维特征的隐向量。换句话说，每个参数 wij=⟨vi,vj⟩wij=⟨vi,vj⟩ w{ij} = \langle \mathbf{v}_i, \mathbf{v}_j \rangle ，这就是 FM 模型的核心思想。因此，FM 的模型方程为（本文不讨论 FM 的高阶形式）

y(x)=w0+∑i=1nwixi+∑i=1n∑j=i+1n⟨vi,vj⟩xixj(2)(2)y(x)=w0+∑i=1nwixi+∑i=1n∑j=i+1n⟨vi,vj⟩xixj y(\mathbf{x}) = w0+ \sum{i=1}^n wi x_i + \sum{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j \label{eq:fm}\tag{2}

其中，vivi \mathbf{v}i 是第 ii i 维特征的隐向量，⟨⋅,⋅⟩⟨⋅,⋅⟩ \langle\cdot, \cdot\rangle 代表向量点积。隐向量的长度为 kk k （k<<nk<<n k << n ），包含 kk k 个描述特征的因子。根据公式 (2)(2)\eqref{eq:fm}，二次项的参数数量减少为 knkn kn 个，远少于多项式模型的参数数量。另外，参数因子化使得 xhxixhxi x_h x_i 的参数和 xixjxixj x_i x_j 的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计 FM 的二次项参数。具体来说，xhxixhxi x_h x_i 和 xixjxixj x_i x_j 的系数分别为 ⟨vh,vi⟩⟨vh,vi⟩ \langle \mathbf{v}_h, \mathbf{v}_i \rangle 和 ⟨vi,vj⟩⟨vi,vj⟩ \langle \mathbf{v}_i, \mathbf{v}_j \rangle ，它们之间有共同项 vivi \mathbf{v}_i 。也就是说，所有包含 “xixi x_i 的非零组合特征”（存在某个 j≠ij≠i j\neq i ，使得 xixj≠0xixj≠0 x_i x_j \neq 0 ）的样本都可以用来学习隐向量 vivi \mathbf{v}_i ，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中，whiwhi w{hi} 和 wijwij w_{ij} 是相互独立的。

显而易见，公式 (2)(2)\eqref{eq:fm}是一个通用的拟合方程，可以采用不同的损失函数用于解决回归、二元分类等问题，比如可以采用 MSE（Mean Square Error）损失函数来求解回归问题，也可以采用 Hinge/Cross-Entropy 损失来求解分类问题。当然，在进行二元分类时，FM 的输出需要经过 sigmoid 变换，这与 Logistic 回归是一样的。直观上看，FM 的复杂度是 O(kn2)O(kn2) O(kn^2) 。但是，通过公式 (3)(3)\eqref{eq:fm_conv}的等式，FM 的二次项可以化简，其复杂度可以优化到 O(kn)O(kn) O(kn) [7]。由此可见，FM 可以在线性时间对新样本作出预测。

∑i=1n∑j=i+1n⟨vi,vj⟩xixj=12∑f=1k⎛⎝⎜⎜(∑i=1nvi,fxi)2−∑i=1nv2i,fx2i⎞⎠⎟⎟(3)(3)∑i=1n∑j=i+1n⟨vi,vj⟩xixj=12∑f=1k((∑i=1nvi,fxi)2−∑i=1nvi,f2xi2) \sum{i=1}^n \sum{j=i+1}^n \langle \mathbf{v}i, \mathbf{v}_j \rangle x_i x_j = \frac{1}{2} \sum{f=1}^k \left(\left( \sum{i=1}^n v{i, f} xi \right)^2 - \sum{i=1}^n v_{i, f}^2 x_i^2 \right) \label{eq:fm_conv}\tag{3}

我们再来看一下 FM 的训练复杂度，利用 SGD（Stochastic Gradient Descent）训练模型。模型各个参数的梯度如下

∂∂θy(x)={1,ifθisw0 xi,ifθiswi xi∑nj=1vj,fxj−vi,fx2i,ifθisvi,f∂∂θy(x)={1,ifθisw0xi,ifθiswixi∑j=1nvj,fxj−vi,fxi2,ifθisvi,f \frac{\partial}{\partial\theta} y (\mathbf{x}) = \left{\begin{array}{ll} 1, & \text{if}\; \theta\; \text{is}\; w0 \ x_i, & \text{if}\; \theta\; \text{is}\; w_i \ x_i \sum{j=1}^n v{j, f} x_j - v{i, f} xi^2, & \text{if}\; \theta\; \text{is}\; v{i, f} \end{array}\right.

其中，vj,fvj,f v{j, f} 是隐向量 vjvj \mathbf{v}_j 的第 ff f 个元素。由于 ∑nj=1vj,fxj∑j=1nvj,fxj \sum{j=1}^n v{j, f} x_j 只与 ff f 有关，而与 ii i 无关，在每次迭代过程中，只需计算一次所有 ff f 的 ∑nj=1vj,fxj∑j=1nvj,fxj \sum{j=1}^n v{j, f} x_j ，就能够方便地得到所有 vi,fvi,f v{i, f} 的梯度。显然，计算所有 ff f 的 ∑nj=1vj,fxj∑j=1nvj,fxj \sum{j=1}^n v{j, f} xj 的复杂度是 O(kn)O(kn) O(kn) ；已知 ∑nj=1vj,fxj∑j=1nvj,fxj \sum{j=1}^n v_{j, f} x_j 时，计算每个参数梯度的复杂度是 O(1)O(1) O(1) ；得到梯度后，更新每个参数的复杂度是 O(1)O(1) O(1) ；模型参数一共有 nk+n+1nk+n+1 nk + n + 1 个。因此，FM 参数训练的复杂度也是 O(kn)O(kn) O(kn) 。综上可知，FM 可以在线性时间训练和预测，是一种非常高效的模型。

FM 与其他模型的对比

FM 是一种比较灵活的模型，通过合适的特征变换方式，FM 可以模拟二阶多项式核的 SVM 模型、MF 模型、SVD++ 模型等 [7]。

相比 SVM 的二阶多项式核而言，FM 在样本稀疏的情况下是有优势的；而且，FM 的训练 / 预测复杂度是线性的，而二项多项式核 SVM 需要计算核矩阵，核矩阵复杂度就是 N 平方。

相比 MF 而言，我们把 MF 中每一项的 rating 分改写为 rui∼βu+γi+xTuyirui∼βu+γi+xuTyi r_{ui} \sim \beta_u + \gamma_i + x_u^T y_i ，从公式 (2)(2)\eqref{eq:fm}中可以看出，这相当于只有两类特征 uu u 和 ii i 的 FM 模型。对于 FM 而言，我们可以加任意多的特征，比如 user 的历史购买平均值，item 的历史购买平均值等，但是 MF 只能局限在两类特征。SVD++ 与 MF 类似，在特征的扩展性上都不如 FM，在此不再赘述。

FFM（Field-aware Factorization Machine）最初的概念来自 Yu-Chin Juan（阮毓钦，毕业于中国台湾大学，现在美国 Criteo 工作）与其比赛队员，是他们借鉴了来自 Michael Jahrer 的论文 [14]中的 field 概念提出了 FM 的升级版模型。通过引入 field 的概念，FFM 把相同性质的特征归于同一个 field。以上面的广告分类为例，“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15” 这三个特征都是代表日期的，可以放到同一个 field 中。同理，商品的末级品类编码生成了 550 个特征，这 550 个特征都是说明商品所属的品类，因此它们也可以放到同一个 field 中。简单来说，同一个 categorical 特征经过 One-Hot 编码生成的数值特征都可以放到同一个 field，包括用户性别、职业、品类偏好等。在 FFM 中，每一维特征 xixi xi ，针对其它特征的每一种 field fjfj f_j ，都会学习一个隐向量 vi,fjvi,fj \mathbf{v}{i, f_j} 。因此，隐向量不仅与特征相关，也与 field 相关。也就是说，“Day=26/11/15”这个特征与 “Country” 特征和 “Ad_type” 特征进行关联的时候使用不同的隐向量，这与 “Country” 和“Ad_type”的内在差异相符，也是 FFM 中 “field-aware” 的由来。

假设样本的 nn n 个特征属于 ff f 个 field，那么 FFM 的二次项有 nfnf nf 个隐向量。而在 FM 模型中，每一维特征的隐向量只有一个。FM 可以看作 FFM 的特例，是把所有特征都归属到一个 field 时的 FFM 模型。根据 FFM 的 field 敏感特性，可以导出其模型方程。

y(x)=w0+∑i=1nwixi+∑i=1n∑j=i+1n⟨vi,fj,vj,fi⟩xixj(4)(4)y(x)=w0+∑i=1nwixi+∑i=1n∑j=i+1n⟨vi,fj,vj,fi⟩xixj y(\mathbf{x}) = w0 + \sum{i=1}^n wi x_i + \sum{i=1}^n \sum{j=i+1}^n \langle \mathbf{v}{i, fj}, \mathbf{v}{j, f_i} \rangle x_i x_j \label{eq:ffm}\tag{4}

其中，fjfj f_j 是第 jj j 个特征所属的 field。如果隐向量的长度为 kk k ，那么 FFM 的二次参数有 nfknfk nfk 个，远多于 FM 模型的 nknk nk 个。此外，由于隐向量与 field 相关，FFM 二次项并不能够化简，其预测复杂度是 O(kn2)O(kn2) O(kn^2) 。

下面以一个例子简单说明 FFM 的特征组合方式 [9]。输入记录如下

User	Movie	Genre	Price
YuChin	3Idiots	Comedy, Drama	$9.99

这条记录可以编码成 5 个特征，其中 “Genre=Comedy” 和“Genre=Drama”属于同一个 field，“Price”是数值型，不用 One-Hot 编码转换。为了方便说明 FFM 的样本格式，我们将所有的特征和对应的 field 映射成整数编号。

Field name	Field index	Feature name	Feature index
User	1	User=YuChin	1
Movie	2	Movie=3Idiots	2
Genre	3	Genre=Comedy	3
Price	4	Genre=Drama	4
		Price	5

那么，FFM 的组合特征有 10 项，如下图所示。

⟨v1,2,v2,1⟩⋅1⋅1+⟨v1,3,v3,1⟩⋅1⋅1+⟨v1,3,v4,1⟩⋅1⋅1+⟨v1,4,v5,1⟩⋅1⋅9.99 +⟨v2,3,v3,2⟩⋅1⋅1+⟨v2,3,v4,2⟩⋅1⋅1+⟨v2,4,v5,2⟩⋅1⋅9.99 +⟨v3,3,v4,3⟩⋅1⋅1+⟨v3,4,v5,3⟩⋅1⋅9.99 +⟨v4,4,v5,3⟩⋅1⋅9.99⟨v1,2,v2,1⟩⋅1⋅1+⟨v1,3,v3,1⟩⋅1⋅1+⟨v1,3,v4,1⟩⋅1⋅1+⟨v1,4,v5,1⟩⋅1⋅9.99+⟨v2,3,v3,2⟩⋅1⋅1+⟨v2,3,v4,2⟩⋅1⋅1+⟨v2,4,v5,2⟩⋅1⋅9.99+⟨v3,3,v4,3⟩⋅1⋅1+⟨v3,4,v5,3⟩⋅1⋅9.99+⟨v4,4,v5,3⟩⋅1⋅9.99 \begin{align*}\begin{array}{r} \langle \mathbf{v}*{{\color{blue}1}, {\color{red}2}}, \mathbf{v}*{{\color{blue}2}, {\color{red}1}} \rangle \cdot {\color{green}1} \cdot {\color{green}1} + \langle \mathbf{v}*{{\color{blue}1}, {\color{red}3}}, \mathbf{v}*{{\color{blue}3}, {\color{red}1}} \rangle \cdot {\color{green}1} \cdot {\color{green}1} + \langle \mathbf{v}*{{\color{blue}1}, {\color{red}3}}, \mathbf{v}*{{\color{blue}4}, {\color{red}1}} \rangle \cdot {\color{green}1} \cdot {\color{green}1} + \langle \mathbf{v}*{{\color{blue}1}, {\color{red}4}}, \mathbf{v}*{{\color{blue}5}, {\color{red}1}} \rangle \cdot {\color{green}1} \cdot {\color{green}{9.99}} \ {} + \langle \mathbf{v}*{{\color{blue}2}, {\color{red}3}}, \mathbf{v}*{{\color{blue}3}, {\color{red}2}} \rangle \cdot {\color{green}1} \cdot {\color{green}1} + \langle \mathbf{v}*{{\color{blue}2}, {\color{red}3}}, \mathbf{v}*{{\color{blue}4}, {\color{red}2}} \rangle \cdot {\color{green}1} \cdot {\color{green}1} + \langle \mathbf{v}*{{\color{blue}2}, {\color{red}4}}, \mathbf{v}*{{\color{blue}5}, {\color{red}2}} \rangle \cdot {\color{green}1} \cdot {\color{green}{9.99}} \ {} + \langle \mathbf{v}*{{\color{blue}3}, {\color{red}3}}, \mathbf{v}*{{\color{blue}4}, {\color{red}3}} \rangle \cdot {\color{green}1} \cdot {\color{green}1} + \langle \mathbf{v}*{{\color{blue}3}, {\color{red}4}}, \mathbf{v}*{{\color{blue}5}, {\color{red}3}} \rangle \cdot {\color{green}1} \cdot {\color{green}{9.99}} \ {} + \langle \mathbf{v}*{{\color{blue}4}, {\color{red}4}}, \mathbf{v}*{{\color{blue}5}, {\color{red}3}} \rangle \cdot {\color{green}1} \cdot {\color{green}{9.99}} \end{array}\end{align*}

其中，红色是 field 编号，蓝色是特征编号，绿色是此样本的特征取值。二次项的系数是通过与特征 field 相关的隐向量点积得到的，二次项共有 n(n−1)2n(n−1)2 \frac{n(n-1)}{2} 个。

Yu-Chin Juan 实现了一个 C++ 版的 FFM 模型，源码可从 Github 下载 [10]。这个版本的 FFM 省略了常数项和一次项，模型方程如下。

ϕ(w,x)=∑j1,j2∈2⟨wj1,f2,wj2,f1⟩xj1xj2(5)(5)ϕ(w,x)=∑j1,j2∈C2⟨wj1,f2,wj2,f1⟩xj1xj2 \phi(\mathbf{w}, \mathbf{x}) = \sum{j_1, j_2 \in \mathcal{C}_2} \langle \mathbf{w}{j1, f_2}, \mathbf{w}{j2, f_1} \rangle x{j1} x{j_2} \label{eq:phi}\tag{5}

其中，2C2 \mathcal{C}2 是非零特征的二元组合，j1j1 j_1 是特征，属于 field f1f1 f_1 ，wj1,f2wj1,f2 \mathbf{w}{j_1, f_2} 是特征 j1j1 j_1 对 field f2f2 f_2 的隐向量。此 FFM 模型采用 logistic loss 作为损失函数，和 L2 惩罚项，因此只能用于二元分类问题。

minw∑i=1Llog(1+exp{−yiϕ(w,xi)})+λ2‖w‖2minw∑i=1Llog⁡(1+exp⁡{−yiϕ(w,xi)})+λ2‖w‖2 \min{\mathbf{w}} \sum{i=1}^L \log \big( 1 + \exp{ -y_i \phi (\mathbf{w}, \mathbf{x}_i ) } \big) + \frac{\lambda}{2} | \mathbf{w} |^2

其中，yi∈{−1,1}yi∈{−1,1} y_i \in {-1, 1} 是第 ii i 个样本的 label，LL L 是训练样本数量，λλ \lambda 是惩罚项系数。模型采用 SGD 优化，优化流程如下。

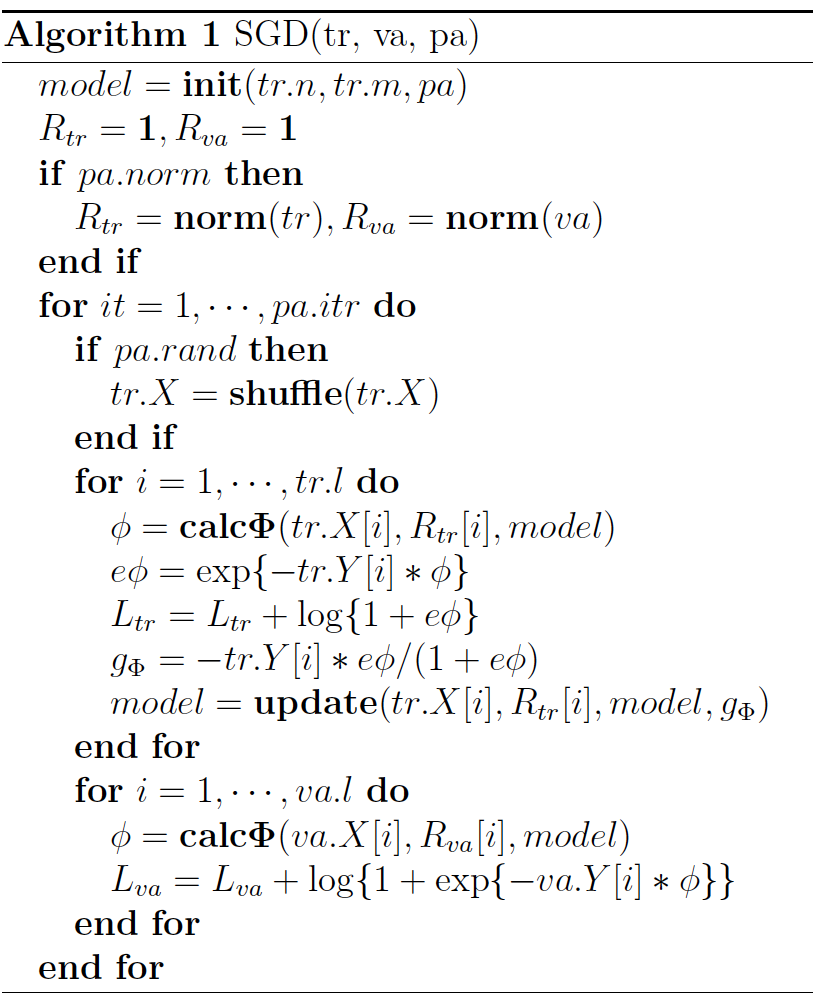
参考 Algorithm1Algorithm1 Algorithm\; 1 , 下面简单解释一下 FFM 的 SGD 优化过程。算法的输入 trtr tr 、vavava、papa pa 分别是训练样本集、验证样本集和训练参数设置。

根据样本特征数量（tr.ntr.n tr.n ）、field 的个数（tr.mtr.m tr.m ）和训练参数（papa pa ），生成初始化模型，即随机生成模型的参数；
如果归一化参数 pa.normpa.norm pa.norm 为真，计算训练和验证样本的归一化系数，样本 ii i 的归一化系数为 R[i]=1‖X[i]‖R[i]=1‖X[i]‖ R[i] = \frac{1}{| \mathbf{X}[i] |}
对每一轮迭代，如果随机更新参数 pa.randpa.rand pa.rand 为真，随机打乱训练样本的顺序；
对每一个训练样本，执行如下操作
- 计算每一个样本的 FFM 项，即公式 (5)(5)\eqref{eq:phi}中的输出 ϕϕ \phi ；
- 计算每一个样本的训练误差，如算法所示，这里采用的是交叉熵损失函数 log(1+eϕ)log⁡(1+eϕ) \log ( 1 + e\phi )；
- 利用单个样本的损失函数计算梯度 gΦgΦ g_\Phi ，再根据梯度更新模型参数；
对每一个验证样本，计算样本的 FFM 输出，计算验证误差；
重复步骤 3~5，直到迭代结束或验证误差达到最小。

在 SGD 寻优时，代码采用了一些小技巧，对于提升计算效率是非常有效的。

第一，梯度分步计算。采用 SGD 训练 FFM 模型时，只采用单个样本的损失函数来计算模型参数的梯度。

=err+reg=log(1+exp{−yiϕ(w,xi)})+λ2‖w‖2L=Lerr+Lreg=log⁡(1+exp⁡{−yiϕ(w,xi)})+λ2‖w‖2 \mathcal{L} = \mathcal{L}_{err} + \mathcal{L}_{reg} = \log \big( 1 + \exp\{ -y*i \phi(\mathbf{w}, \mathbf{x}\_i )\} \big) + \frac{\lambda}{2} \| \mathbf{w} \|^2 ∂∂w=∂err∂ϕ⋅∂ϕ∂w+∂reg∂w∂L∂w=∂Lerr∂ϕ⋅∂ϕ∂w+∂Lreg∂w \frac{\partial\mathcal{L}}{\partial\mathbf{w}} = \frac{\partial\mathcal{L}*{err}}{\partial\phi}\cdot \frac{\partial\phi}{\partial\mathbf{w}} + \frac{\partial\mathcal{L}\_{reg}}{\partial\mathbf{w}}

上面的公式表明，∂err∂ϕ∂Lerr∂ϕ \frac{\partial\mathcal{L}{err}}{\partial\phi} 与具体的模型参数无关。因此，每次更新模型时，只需计算一次，之后直接调用 ∂err∂ϕ∂Lerr∂ϕ \frac{\partial\mathcal{L}{err}}{\partial\phi} 的值即可。对于更新 nfknfk nfk 个模型参数，这种方式能够极大提升运算效率。

第二，自适应学习率。此版本的 FFM 实现没有采用常用的指数递减的学习率更新策略，而是利用 nfknfk nfk 个浮点数的临时空间，自适应地更新学习率。学习率是参考 AdaGrad 算法计算的 [11]，按如下方式更新

w‘j1,f2=wj1,f2−η1+∑t(gtwj1,f2)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾√⋅gwj1,f2wj1,f2‘=wj1,f2−η1+∑t(gwj1,f2t)2⋅gwj1,f2 w^{‘}_{j_1, f_2} = w_{j*1, f_2} - \frac{\eta}{\sqrt{1 + \sum_t (g^t*{w*{j_1, f_2}})^2 }}\cdot g*{w\_{j_1, f_2}}

其中，wj1,f2wj1,f2 w{j_1, f_2} 是特征 j1j1 j_1 对 field f2f2 f_2 隐向量的一个元素，元素下标未标出；gwj1,f2gwj1,f2 g{w{j_1, f_2}} 是损失函数对参数 wj1,f2wj1,f2 w{j1, f_2} 的梯度；gtwj1,f2gwj1,f2t g^t{w_{j_1, f_2}} 是第 tt t 次迭代的梯度；ηη \eta 是初始学习率。可以看出，随着迭代的进行，每个参数的历史梯度会慢慢累加，导致每个参数的学习率逐渐减小。另外，每个参数的学习率更新速度是不同的，与其历史梯度有关，根据 AdaGrad 的特点，对于样本比较稀疏的特征，学习率高于样本比较密集的特征，因此每个参数既可以比较快速达到最优，也不会导致验证误差出现很大的震荡。

第三，OpenMP 多核并行计算。OpenMP 是用于共享内存并行系统的多处理器程序设计的编译方案，便于移植和多核扩展 [12]。FFM 的源码采用了 OpenMP 的 API，对参数训练过程 SGD 进行了多线程扩展，支持多线程编译。因此，OpenMP 技术极大地提高了 FFM 的训练效率和多核 CPU 的利用率。在训练模型时，输入的训练参数 ns_threads 指定了线程数量，一般设定为 CPU 的核心数，便于完全利用 CPU 资源。

第四，SSE3 指令并行编程。SSE3 全称为数据流单指令多数据扩展指令集 3，是 CPU 对数据层并行的关键指令，主要用于多媒体和游戏的应用程序中 [13]。SSE3 指令采用 128 位的寄存器，同时操作 4 个单精度浮点数或整数。SSE3 指令的功能非常类似于向量运算。例如，aa a 和 bb b 采用 SSE3 指令相加（aa a 和 bb b 分别包含 4 个数据），其功能是 aa a 中的 4 个元素与 bb b 中 4 个元素对应相加，得到 4 个相加后的值。采用 SSE3 指令后，向量运算的速度更加快捷，这对包含大量向量运算的 FFM 模型是非常有利的。

除了上面的技巧之外，FFM 的实现中还有很多调优技巧需要探索。例如，代码是按 field 和特征的编号申请参数空间的，如果选取了非连续或过大的编号，就会造成大量的内存浪费；在每个样本中加入值为 1 的新特征，相当于引入了因子化的一次项，避免了缺少一次项带来的模型偏差等。

在 DSP 的场景中，FFM 主要用来预估站内的 CTR 和 CVR，即一个用户对一个商品的潜在点击率和点击后的转化率。

CTR 和 CVR 预估模型都是在线下训练，然后用于线上预测。两个模型采用的特征大同小异，主要有三类：用户相关的特征、商品相关的特征、以及用户 - 商品匹配特征。用户相关的特征包括年龄、性别、职业、兴趣、品类偏好、浏览 / 购买品类等基本信息，以及用户近期点击量、购买量、消费额等统计信息。商品相关的特征包括所属品类、销量、价格、评分、历史 CTR/CVR 等信息。用户 - 商品匹配特征主要有浏览 / 购买品类匹配、浏览 / 购买商家匹配、兴趣偏好匹配等几个维度。

为了使用 FFM 方法，所有的特征必须转换成 “field_id:feat_id:value” 格式，field_id 代表特征所属 field 的编号，feat_id 是特征编号，value 是特征的值。数值型的特征比较容易处理，只需分配单独的 field 编号，如用户评论得分、商品的历史 CTR/CVR 等。categorical 特征需要经过 One-Hot 编码成数值型，编码产生的所有特征同属于一个 field，而特征的值只能是 0 或 1，如用户的性别、年龄段，商品的品类 id 等。除此之外，还有第三类特征，如用户浏览 / 购买品类，有多个品类 id 且用一个数值衡量用户浏览或购买每个品类商品的数量。这类特征按照 categorical 特征处理，不同的只是特征的值不是 0 或 1，而是代表用户浏览或购买数量的数值。按前述方法得到 field_id 之后，再对转换后特征顺序编号，得到 feat_id，特征的值也可以按照之前的方法获得。

CTR、CVR 预估样本的类别是按不同方式获取的。CTR 预估的正样本是站内点击的用户 - 商品记录，负样本是展现但未点击的记录；CVR 预估的正样本是站内支付（发生转化）的用户 - 商品记录，负样本是点击但未支付的记录。构建出样本数据后，采用 FFM 训练预估模型，并测试模型的性能。

	#(field)	#(feature)	AUC	Logloss
站内 CTR	39	2456	0.77	0.38
站内 CVR	67	2441	0.92	0.13

由于模型是按天训练的，每天的性能指标可能会有些波动，但变化幅度不是很大。这个表的结果说明，站内 CTR/CVR 预估模型是非常有效的。

在训练 FFM 的过程中，有许多小细节值得特别关注。

第一，样本归一化。FFM 默认是进行样本数据的归一化，即 pa.normpa.norm pa.norm 为真；若此参数设置为假，很容易造成数据 inf 溢出，进而引起梯度计算的 nan 错误。因此，样本层面的数据是推荐进行归一化的。

第二，特征归一化。CTR/CVR 模型采用了多种类型的源特征，包括数值型和 categorical 类型等。但是，categorical 类编码后的特征取值只有 0 或 1，较大的数值型特征会造成样本归一化后 categorical 类生成特征的值非常小，没有区分性。例如，一条用户 - 商品记录，用户为 “男” 性，商品的销量是 5000 个（假设其它特征的值为零），那么归一化后特征 “sex=male”（性别为男）的值略小于 0.0002，而“volume”（销量）的值近似为 1。特征“sex=male” 在这个样本中的作用几乎可以忽略不计，这是相当不合理的。因此，将源数值型特征的值归一化到 [0,1][0,1] [0, 1] 是非常必要的。

第三，省略零值特征。从 FFM 模型的表达式 (4)(4)\eqref{eq:ffm}可以看出，零值特征对模型完全没有贡献。包含零值特征的一次项和组合项均为零，对于训练模型参数或者目标值预估是没有作用的。因此，可以省去零值特征，提高 FFM 模型训练和预测的速度，这也是稀疏样本采用 FFM 的显著优势。

本文主要介绍了 FFM 的思路来源和理论原理，并结合源码说明 FFM 的实际应用和一些小细节。从理论上分析，FFM 的参数因子化方式具有一些显著的优势，特别适合处理样本稀疏性问题，且确保了较好的性能；从应用结果来看，站内 CTR/CVR 预估采用 FFM 是非常合理的，各项指标都说明了 FFM 在点击率预估方面的卓越表现。当然，FFM 不一定适用于所有场景且具有超越其他模型的性能，合适的应用场景才能成就 FFM 的 “威名”。